Piramit bir prizma ile birlikte üç boyutlu uzayda mükemmel bir çokyüzlüdür, geometrik özellikleri lisede incelenir. Bu yazıda piramitlerin ne olduğunu, hangi unsurlardan oluştuğunu ele alacağız ve ayrıca doğru piramitleri kısaca karakterize edeceğiz.
Geometrik figür piramidi
Geometri açısından piramit, bir çokgen ve birkaç üçgenden oluşan uzamsal bir şekildir. Bu rakamı elde etmek oldukça basittir. Bunu yapmak için, n kenarlı bir çokgen alın, sonra çokgenin düzleminde yer almayan uzayda keyfi bir nokta seçin ve çokgenin her bir köşesini bu noktaya bağlayın. Açıkçası, bu şekilde oluşturulan şeklin bir köşe noktasında birbirine bağlı n tane üçgeni olacaktır.
Tarif edilen şeklin geometrik şeklini görselleştirmek için bir resim çekelim.

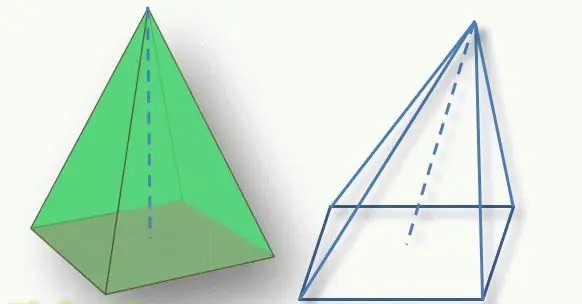
Bu, tabanı dörtgen olan bir piramidi gösterir.dörtgendir ve yan yüzey, ortak bir tepe noktasına sahip dört üçgenden oluşur.
Piramit öğeleri
Her çokyüzlü gibi, piramit de üç tür öğeden oluşur:
- kenarlar;
- üstler;
- kaburga.
Yüzler, bir şeklin iç hacmini çevreleyen alandan ayıran düzlem parçalarıdır. Piramidin tabanında bir n-gon varsa, yüzlerinin sayısı her zaman n+1'dir. Bunlardan n kenarı üçgendir ve bir kenarı bahsedilen n-köşeli tabandır.
Köşeler, bir şeklin üç veya daha fazla yüzünün kesiştiği noktalardır. Taban bölgesi, her biri iki üçgen yüz ve bir tabandan oluşan n tane köşe içerir. n tane üçgen kenarın birleştiği noktaya piramidin tepesi denir. Böylece, incelenen şekil n+1 köşeden oluşur.
Kenarlar, iki yüz kesiştiğinde görünen düz çizgilerdir. Her kenar, uçlarında iki köşe ile sınırlandırılmıştır. N-gon tabanlı herhangi bir piramit 2n kenar içerir. Bu sayının yarısı yani n sadece yan üçgenlerin kesişiminden oluşur.
Olası şekil türleri
İncelenen şeklin adı, tabandaki çokgen türüne göre benzersiz bir şekilde belirlenir. Örneğin, üç köşesi ve üç kenarı varsa, o zaman piramit üçgen, dört ise - dörtgen vb. olacaktır.
Poligon dışbükey ve içbükey olabileceği gibi normal ve genel tipte olabilir. Bütün bunlar aynı zamanda piramidin görünümünü de belirler.
Figür türünü belirlemede önemli bir nokta, piramidin tepesinin tabanına göre konumudur. Üstten çokgen tabana çizilen dik parçaya şeklin yüksekliği denir. Bu segment, tabanı geometrik merkezinde kesişirse (bir üçgen için bu, medyanların kesişimidir, bir dörtgen için köşegenlerin kesişimidir), o zaman şekle düz bir çizgi denir. Aksi takdirde eğimli bir piramitten bahsederler.
Tabanın n-gonu düzgünse (eşkenar üçgen, kare vb.) ve şekil düzse buna düzgün piramit denir.
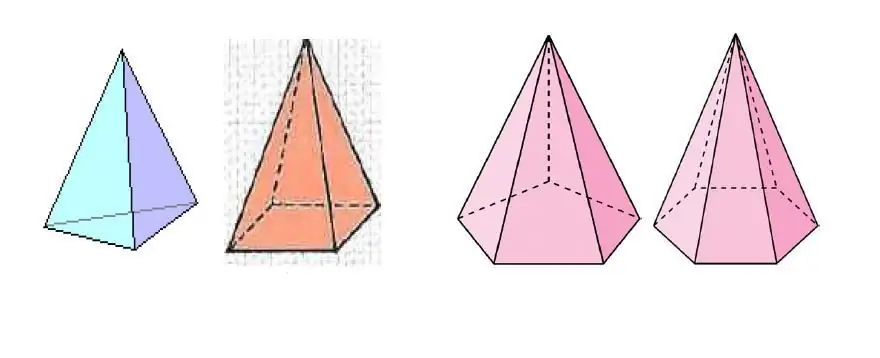
Yukarıdaki resim, tabandaki çokgenin kenar sayısı bakımından farklılık gösteren birkaç piramidi göstermektedir.
Düzenli piramitlerin özellikleri
Bu piramitler, bu sınıftaki diğer figürlerden yüksek derecede simetri ile farklıdır. Bu bağlamda, bunlarla hacim veya yüzey alanı gibi çeşitli geometrik hesaplamalar yapmak uygundur.
Düzenli bir piramit, tabanında, kenarının uzunluğu bilgisinden benzersiz bir şekilde belirlenen bir n-gon içerir. Şeklin yan yüzeyi, eşkenar olan n adet özdeş üçgenden oluşur. Yan yüzeyde bulunan düzgün bir piramidin kenarları birbirine eşittir. Bu kenarın uzunluk değeri genellikle bir şeklin özünü hesaplarken ve yüzey alanını belirlerken kullanılır.
Düzenli bir piramidin yüksekliği, şeklin ikinci önemli özelliğidir (birincisi, kenarın uzunluğudur).gerekçesiyle). Hacim hesaplanırken yükseklik kullanılır.
Piramidin yan yüzlerini kesen tabana paralel herhangi bir düzlem çokgen bir bölümün oluşmasına yol açar. Taban çokgenine göre homotetiktir. Tanımlanan dilim işlemi, tüm bir yeni şekiller sınıfının oluşmasına yol açar - kesik düzenli piramitler.
En ünlü piramitler

Elbette bunlar Mısır firavunlarının düzenli dörtgen piramitleri. Giza adlı bir yerde, tasarımın mükemmelliği ve geometrik parametrelerinin doğruluğu bilim adamlarını bugüne kadar şaşırtmaya devam eden bu taş anıtlardan 100'den fazla var. Bunların en büyüğü, yaklaşık 146 metre yüksekliğinde ve yaklaşık 230 metre uzunluğunda olan Keops Piramidi'dir.
Bu piramitlerin tam olarak ne işe yaradığının yanı sıra hangi mekanizmalarla ve ne zaman inşa edildiklerini bugüne kadar kimse bilmiyor.






