İdeal gaz, ideal gaz hal denklemi, sıcaklığı ve basıncı, hacmi… Fiziğin ilgili bölümünde kullanılan parametreler ve tanımlar listesi oldukça uzun bir süre devam ettirilebilir. Bugün sadece bu konu hakkında konuşacağız.
Moleküler fizikte ne düşünülür?

Bu bölümde ele alınan ana nesne ideal bir gazdır. İdeal gaz hal denklemi normal çevre koşulları dikkate alınarak elde edildi ve bundan biraz sonra bahsedeceğiz. Şimdi bu "soruna" uzaktan yaklaşalım.
Diyelim ki bir miktar gazımız var. Durumu, termodinamik yapıdaki üç parametre kullanılarak belirlenebilir. Bunlar elbette basınç, hacim ve sıcaklıktır. Bu durumda sistemin durum denklemi, karşılık gelen parametreler arasındaki ilişkinin formülü olacaktır. Şuna benziyor: F (p, V, T)=0.
Burada, ilk kez, ideal diye bir şeyin ortaya çıkmasına yavaş yavaş yaklaşıyoruz.gaz. Moleküller arasındaki etkileşimlerin ihmal edilebilir olduğu bir gaz olarak adlandırılır. Genel olarak, bu doğada yoktur. Bununla birlikte, oldukça nadir bulunan herhangi bir gaz ona yakındır. Normal şartlar altında bulunan azot, oksijen ve hava idealden çok az farklıdır. İdeal bir gazın hal denklemini yazmak için birleşik gaz yasasını kullanabiliriz. Şunu elde ederiz: pV/T=const.
İlgili Kavram 1: Avogadro Yasası
Herhangi bir rastgele gazın aynı sayıda molünü alırsak ve bunları sıcaklık ve basınç dahil olmak üzere aynı koşullara koyarsak, gazların aynı hacmi işgal edeceğini söyleyebilir. Özellikle, deney normal koşullar altında gerçekleştirilmiştir. Bu, sıcaklığın 273.15 Kelvin, basıncın bir atmosfer (760 milimetre cıva veya 101325 Paskal) olduğu anlamına gelir. Bu parametrelerle, gaz 22.4 litreye eşit bir hacim işgal etti. Bu nedenle, herhangi bir gazın bir molü için sayısal parametrelerin oranının sabit bir değer olacağını söyleyebiliriz. Bu yüzden bu rakamı R harfi ile belirlemeye ve evrensel gaz sabiti olarak adlandırmaya karar verildi. Böylece 8.31'e eşittir. Birimi J/molK'dir.
İdeal gaz. İdeal gaz hal denklemi ve manipülasyonu
Formülü yeniden yazmaya çalışalım. Bunu yapmak için şu formda yazıyoruz: pV=RT. Ardından, basit bir eylem gerçekleştiriyoruz, denklemin her iki tarafını da keyfi sayıda mol ile çarpıyoruz. pVu=uRT elde ederiz. Molar hacmin çarpımının vemaddenin miktarı sadece hacimdir. Ama sonuçta, mol sayısı aynı anda kütlenin ve molar kütlenin bölümüne eşit olacaktır. Mendeleev-Clapeyron denklemi tam olarak böyle görünüyor. İdeal bir gazın nasıl bir sistem oluşturduğu konusunda net bir fikir verir. İdeal bir gazın hal denklemi şu şekilde olacaktır: pV=mRT/M.
Basınç formülünü çıkar
Elde edilen ifadelerle biraz daha manipülasyon yapalım. Bunu yapmak için Mendeleev-Clapeyron denkleminin sağ tarafı Avogadro sayısı ile çarpılır ve bölünür. Şimdi madde miktarının ürününe Avogadro sayısı ile dikkatlice bakıyoruz. Bu, gazdaki toplam molekül sayısından başka bir şey değildir. Ancak aynı zamanda evrensel gaz sabitinin Avogadro sayısına oranı Boltzmann sabitine eşit olacaktır. Bu nedenle basınç formülleri şu şekilde yazılabilir: p=NkT/V veya p=nkT. Burada n sembolü parçacık konsantrasyonudur.
İdeal gaz süreçleri
Moleküler fizikte izoprosesler diye bir şey vardır. Bunlar, sistemde sabit parametrelerden birinde gerçekleşen termodinamik süreçlerdir. Bu durumda maddenin kütlesi de sabit kalmalıdır. Onlara daha spesifik olarak bakalım. Yani, ideal bir gazın yasaları.
Basınç sabit kalır
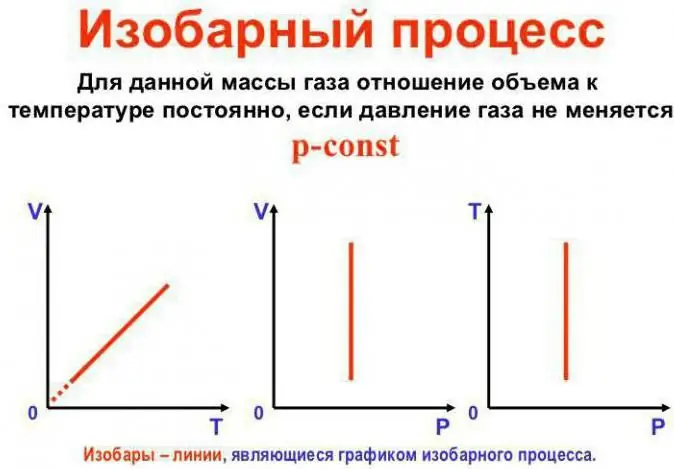
Bu Gay-Lussac yasasıdır. Şuna benziyor: V/T=const. Başka bir şekilde yeniden yazılabilir: V=Vo (1 + at). Burada a, 1/273.15 K^-1'e eşittir ve "hacim genişleme katsayısı" olarak adlandırılır. Sıcaklığı hem Celsius hem deKelvin ölçeği. İkinci durumda, V=Voat formülünü elde ederiz.
Ses sabit kalır

Bu, Gay-Lussac'ın ikinci yasasıdır ve daha yaygın olarak Charles yasası olarak adlandırılır. Şuna benziyor: p/T=const. Başka bir formülasyon daha var: p=po (1 + at). Dönüşümler önceki örneğe göre gerçekleştirilebilir. Gördüğünüz gibi, ideal gaz yasaları bazen birbirine oldukça benzer.
Sıcaklık sabit kalır

İdeal bir gazın sıcaklığı sabit kalırsa, Boyle-Mariotte yasasını elde edebiliriz. Şu şekilde yazılabilir: pV=const.
İlgili Kavram 2: Kısmi Basınç
Diyelim ki gazlı bir gemimiz var. Karışım olacak. Sistem bir termal denge durumundadır ve gazların kendileri birbirleriyle reaksiyona girmez. Burada N, toplam molekül sayısını gösterecektir. Sırasıyla N1, N2 ve benzeri, karışımın bileşenlerinin her birindeki molekül sayısı. p=nkT=NkT/V basınç formülünü alalım. Belirli bir dava için açılabilir. İki bileşenli bir karışım için formül şu şekilde olacaktır: p=(N1 + N2) kT/V. Ama sonra, toplam basıncın, her karışımın kısmi basınçlarından toplanacağı ortaya çıkıyor. Yani, p1 + p2 ve benzeri gibi görünecek. Bunlar kısmi baskılar olacak.
Ne için?
Elde ettiğimiz formül, sistemdeki basıncın her molekül grubundan olduğunu gösteriyor. Bu arada, buna bağlı değildiğerleri. D alton, daha sonra kendi adıyla anılacak olan yasayı formüle ederken bundan yararlandı: gazların birbirleriyle kimyasal olarak reaksiyona girmediği bir karışımda, toplam basınç, kısmi basınçların toplamına eşit olacaktır.






