Doğrusal bir işlev, bir yüzey boyunca çizilen düz bir çizgidir. Farklı tip ve modellere ayrılabilir. Aşağıda, onu elde etmenin formüllerini ve aynı zamanda düzlemde mükemmelliğini elde etmeyi ele alacağız. Çizimlerde bunu tam olarak doğrulayabilir ve nasıl görünmesi gerektiğini anlayabilirsiniz.
Doğrusal fonksiyon y=kx + b
Bu değer, bir görünümdeki bir değişkenin doğru bir ölçüsüdür. Artış, doğrusal bir fonksiyonun temel özelliğini ifade eder, artan argümanla orantılı hale gelir. Başka bir deyişle, fonksiyon doğrudan orantılılığın bir genellemesini temsil eder. Düz bir çizgi, doğrusal bir fonksiyonun grafiğidir. Adı da buradan gelmektedir. Bir gerçek değişken başka bir gerçek işleve dokunur.
Özellikler
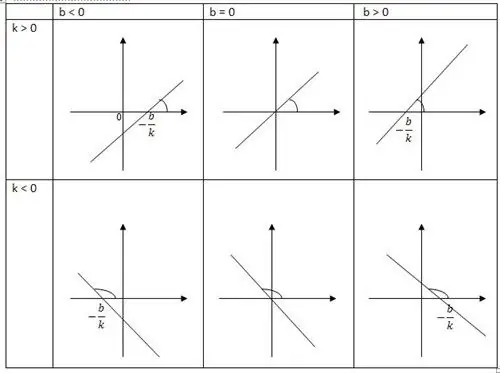
Doğrusal işlev, x ekseninin pozitif yönüne sahip olan düz bir çizginin bir türevidir. Tanımlayıcı eğim faktörlerinden biri k'dir, a açısının tanjantını belirler. X ekseninin pozitif yönünde oluşan düz çizgi k'dir. Diğer b koordinatı isenokta koordinatlarının yanı sıra çizginin eksenle kesişimi.
Doğrusal olmayan işlevler nelerdir?
Doğrusal olmayan işlevlere doğrusal olmayan denir. Bu, değişkenler arasındaki matematiksel bir ilişkidir. Doğrusal olmayanlar y=ax + b şeklinde ifade edilemez. Bu terim, genel durumu incelemenin gerekli olduğu anlarda kullanılır. Bu süreç daha düşük derecelerle başlar. Bu durumda, ikinci dereceden düzeltmeler dikkate alınır. Böyle bir fonksiyon sürekli eğriliğe sahiptir.
Değerlendirilen doğrusal olmayan denklem keyfidir. Doğrusal olmayan bir fonksiyona örnek olarak y=x2 verilebilir. "Doğrusal fonksiyon" terimleri, genellikle bir iyileştirme ve "homojen" eklenmesiyle kullanılır. Bir vektör uzayı olan X'in tam doğrusal eşlemesine uygulanabilir. Doğrusal bir fonksiyon, tüm sistemin buna benzer.






