Ohm Yasası, elektrik devrelerinin temel yasasıdır. Aynı zamanda birçok doğa olayını açıklamamıza da olanak tanır. Örneğin, elektriğin neden tellere oturan kuşları "dövmediği" anlaşılabilir. Fizik için Ohm yasası son derece önemlidir. Onun bilgisi olmadan, kararlı elektrik devreleri oluşturmak imkansız olurdu ya da hiç elektronik olmazdı.
Bağımlılık I=I(U) ve değeri
Malzemelerin direncinin keşfinin tarihi, doğrudan akım-voltaj karakteristiği ile ilgilidir. Ne olduğunu? Sabit bir elektrik akımına sahip bir devre alalım ve elemanlarından herhangi birini düşünelim: bir lamba, bir gaz borusu, bir metal iletken, bir elektrolit şişesi, vb.
Söz konusu elemana sağlanan U gerilimini (genellikle V olarak anılır) değiştirerek, içinden geçen akımın (I) gücündeki değişimi izleyeceğiz. Sonuç olarak, "elementin voltaj özelliği" olarak adlandırılan ve onun doğrudan bir göstergesi olan I \u003d I (U) formunun bir bağımlılığını elde edeceğiz.elektriksel özellikler.
V/A karakteristiği farklı öğeler için farklı görünebilir. En basit şekli, Georg Ohm (1789 - 1854) tarafından yapılan bir metal iletken düşünülerek elde edilir.
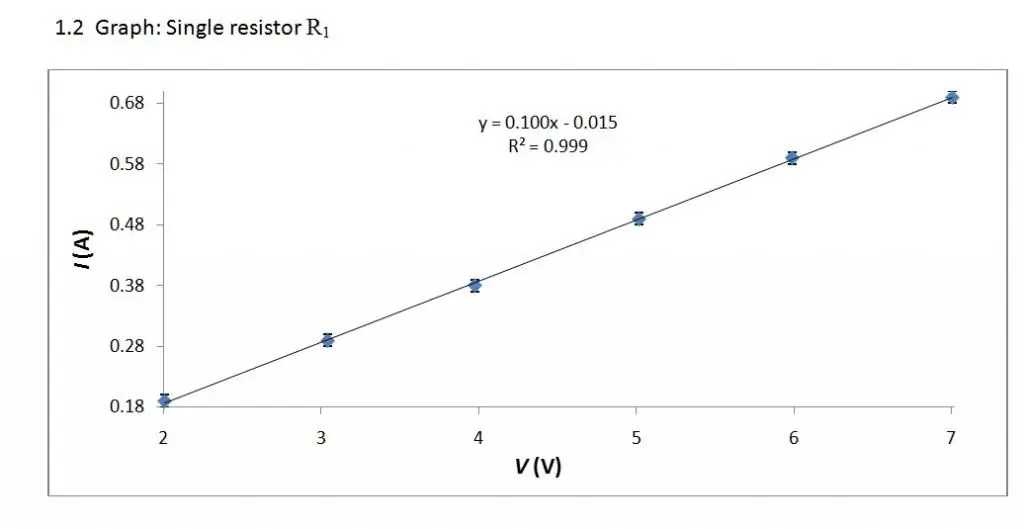
Volt-amper özelliği doğrusal bir ilişkidir. Bu nedenle grafiği düz bir çizgidir.
Yasanın en basit hali
Ohm'un iletkenlerin akım-voltaj özellikleri üzerine yaptığı araştırma, metal bir iletken içindeki akım gücünün uçlarındaki potansiyel farkla (I ~ U) orantılı olduğunu ve belirli bir katsayı ile ters orantılı olduğunu gösterdi, yani I ~ 1/R. Bu katsayı "iletken direnci" olarak bilinir hale geldi ve elektrik direncinin ölçü birimi Ohm veya V/A idi.
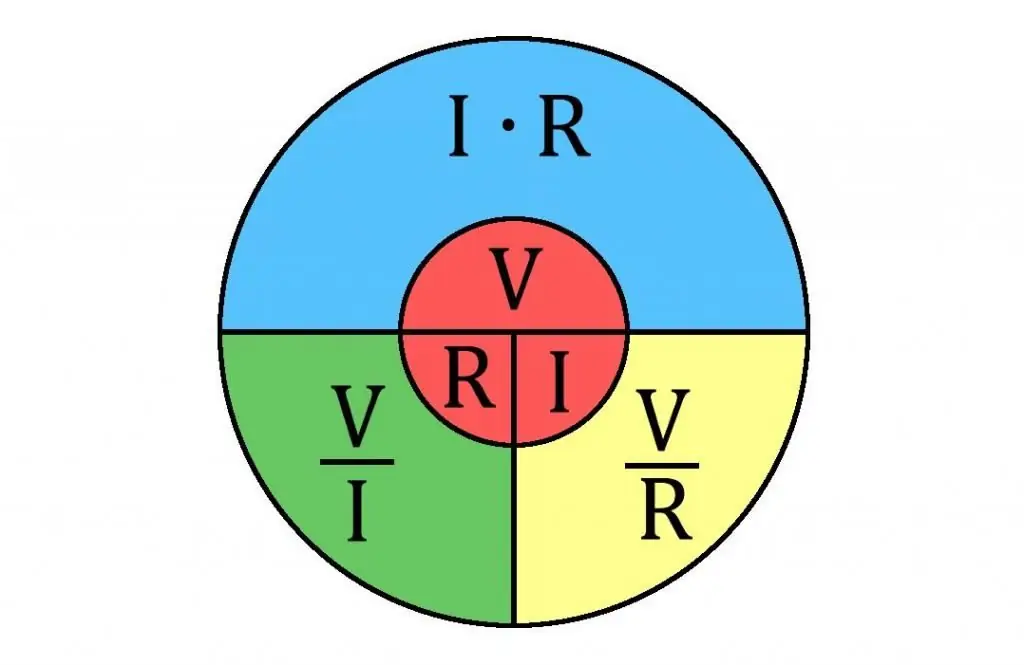
Dikkat edilmesi gereken bir şey daha var. Ohm yasası genellikle devrelerdeki direnci hesaplamak için kullanılır.
Yasa ifadeleri
Ohm Yasası, devrenin tek bir bölümünün akım gücünün (I) bu bölümdeki voltajla orantılı ve direnciyle ters orantılı olduğunu söyler.
Bu formda yasanın yalnızca zincirin homojen bir bölümü için geçerli olduğuna dikkat edilmelidir. Homojen, elektrik devresinin bir akım kaynağı içermeyen kısmıdır. Ohm yasasının homojen olmayan bir devrede nasıl kullanılacağı aşağıda tartışılacaktır.
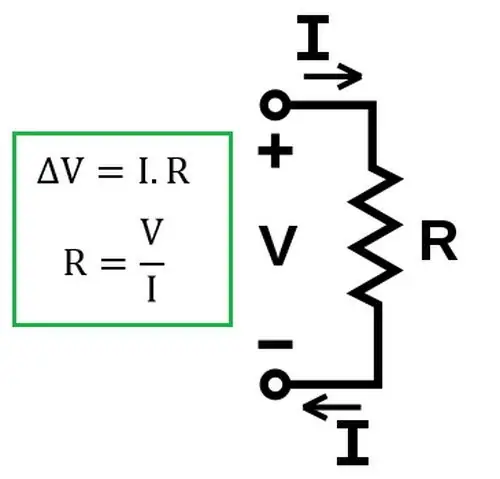
Daha sonra, yasanın çözümler için geçerli olduğu deneysel olarak tespit edildibir elektrik devresindeki elektrolitler.
Direncin fiziksel anlamı
Direnç, elektrik akımının geçişini önlemek için malzemelerin, maddelerin veya ortamların bir özelliğidir. Nicel olarak, 1 ohm'luk bir direnç, uçlarında 1 V gerilim bulunan bir iletkende 1 A'lık bir elektrik akımının geçebileceği anlamına gelir.
Elektrik direnci
Deneysel olarak, iletkenin elektrik akımının direncinin boyutlarına bağlı olduğu bulundu: uzunluk, genişlik, yükseklik. Ve ayrıca şekli (küre, silindir) ve yapıldığı malzeme üzerinde. Böylece, örneğin homojen bir silindirik iletkenin özdirenç formülü şöyle olacaktır: R \u003d pl / S.
Bu formülde s=1 m2 ve l=1 m koyarsak, R sayısal olarak p'ye eşit olacaktır. Buradan, SI cinsinden iletkenin direnç katsayısının ölçü birimi hesaplanır - bu Ohmm.

Özdirenç formülünde p, iletkenin yapıldığı malzemenin kimyasal özelliklerine göre belirlenen direnç katsayısıdır.
Ohm yasasının diferansiyel biçimini düşünmek için birkaç kavramı daha ele almamız gerekiyor.
Akım yoğunluğu
Bildiğiniz gibi, elektrik akımı herhangi bir yüklü parçacığın kesinlikle düzenli bir hareketidir. Örneğin metallerde akım taşıyıcıları elektronlardır ve iletken gazlarda iyonlardır.
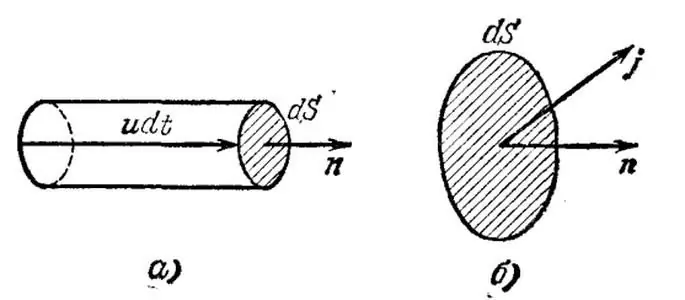
Tüm mevcut taşıyıcılarhomojen - metal iletken. Bu iletkendeki sonsuz küçük bir hacmi zihinsel olarak seçelim ve verilen hacimdeki elektronların ortalama (sapma, sıralı) hızını u ile gösterelim. Ayrıca, n birim hacim başına akım taşıyıcılarının konsantrasyonunu göstersin.
Şimdi, u vektörüne dik sonsuz küçük bir dS alanı çizelim ve hız boyunca, yüksekliği udt olan sonsuz küçük bir silindir oluşturalım; burada dt, dikkate alınan hacimde bulunan tüm mevcut hız taşıyıcılarının geçeceği süreyi gösterir. dS alanı boyunca.
Bu durumda, q=neudSdt'ye eşit yük, e'nin elektron yükü olduğu alan boyunca elektronlar tarafından aktarılacaktır. Böylece, elektrik akımı yoğunluğu, bir birim alan boyunca birim zamanda aktarılan yük miktarını gösteren j=neu vektörüdür.
Ohm Yasası diferansiyel tanımının faydalarından biri, çoğu zaman direnci hesaplamadan başa çıkabilmenizdir.
Elektrik yükü. Elektrik alan şiddeti
Elektrik yükü ile birlikte alan gücü, elektrik teorisinde temel bir parametredir. Aynı zamanda, okul çocukları için mevcut olan basit deneylerden niceliksel bir fikir elde edilebilir.
Basit olması için bir elektrostatik alanı ele alacağız. Bu zamanla değişmeyen bir elektrik alanıdır. Böyle bir alan, sabit elektrik yükleriyle oluşturulabilir.
Ayrıca, amaçlarımız için bir test ücreti gereklidir. Kapasitesi dahilinde, şarjlı bir gövde kullanacağız - o kadar küçük ki, neden olma yeteneğine sahip değil.çevreleyen nesnelerde herhangi bir bozulma (yüklerin yeniden dağılımı).
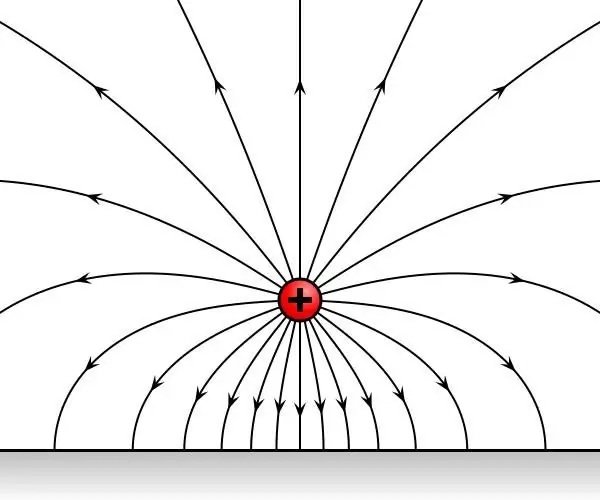
Sırasıyla, bir elektrostatik alanın etkisi altındaki uzayda bir noktaya ardışık olarak yerleştirilmiş iki test yükünü ele alalım. Suçlamaların onun tarafında zamanla değişmeyen bir etkiye maruz kalacağı ortaya çıktı. F1 ve F2 yüklere etki eden kuvvetler olsun.
Deneysel verilerin genelleştirilmesi sonucunda, F1 ve F2 kuvvetlerinin ya bir ya da ve F1/F2 oranları, uzayda test yüklerinin dönüşümlü olarak yerleştirildiği noktadan bağımsızdır. Bu nedenle, F1/F2 oranı, yüklerin kendilerinin bir özelliğidir ve alana bağlı değildir.
Bu gerçeğin keşfi, cisimlerin elektriklenmesini karakterize etmeyi mümkün kıldı ve daha sonra elektrik yükü olarak adlandırıldı. Böylece, tanım olarak, q1/q2=F1/F çıkıyor 2 , burada q1 ve q2 - alanın bir noktasına yerleştirilen yüklerin miktarı ve F 1 ve F2 - alanın kenarından yüklere etki eden kuvvetler.
Bu tür düşüncelerden yola çıkarak, çeşitli parçacıkların yüklerinin büyüklükleri deneysel olarak belirlendi. Orandaki test yüklerinden birini koşullu olarak bire eşitleyerek, F1/F2 oranını ölçerek diğer yükün değerini hesaplayabilirsiniz..
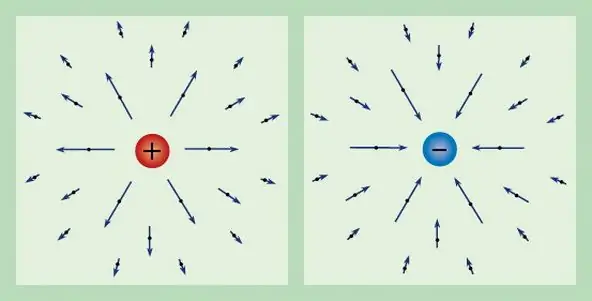
Herhangi bir elektrik alanı, bilinen bir yük ile karakterize edilebilir. Böylece, hareketsiz durumdaki bir birim test yüküne etki eden kuvvete elektrik alan kuvveti denir ve E ile gösterilir. Yükün tanımından, kuvvet vektörünün aşağıdaki forma sahip olduğunu elde ederiz: E=F/q.
j ve E vektörlerinin bağlantısı. Ohm yasasının başka bir şekli
Homojen bir iletkende, yüklü parçacıkların düzenli hareketi E vektörü yönünde gerçekleşecektir. Bu, j ve E vektörlerinin birlikte yönlendirileceği anlamına gelir. Akım yoğunluğunu belirlerken olduğu gibi, iletkende sonsuz küçük silindirik bir hacim seçiyoruz. Daha sonra bu silindirin kesitinden jdS'ye eşit bir akım geçecek ve silindire uygulanan voltaj Edl'ye eşit olacaktır. Bir silindirin özdirenç formülü de bilinir.
Ardından, akım kuvvetinin formülünü iki şekilde yazarak şunu elde ederiz: j=E/p, burada 1/p değerine elektriksel iletkenlik denir ve elektrik özdirencinin tersidir. Genellikle σ (sigma) veya λ (lambda) ile gösterilir. İletkenlik birimi Sm/m'dir, burada Sm Siemens'tir. Ohm'un birim tersi.
Böylece, homojen olmayan bir devre için Ohm yasası hakkında yukarıda sorulan soruyu cevaplayabiliriz. Bu durumda, akım taşıyıcıları, E1 yoğunluğu ile karakterize edilen elektrostatik alandan gelen kuvvetten ve bunlara etki eden başka bir akım kaynağından gelen diğer kuvvetlerden etkilenecektir. E 2 olarak belirlenmiştir. Sonra Ohm Yasası uygulandızincirin homojen olmayan bölümü şöyle görünecektir: j=λ(E1 + E2).
İletkenlik ve Direnç hakkında daha fazla bilgi
Bir iletkenin bir elektrik akımını iletme yeteneği, özdirenç formülü ile bulunabilen özdirenci veya iletkenliğin tersi olarak hesaplanan iletkenlik ile karakterize edilir. Bu parametrelerin değeri hem iletken malzemenin kimyasal özellikleri hem de dış koşullar tarafından belirlenir. Özellikle ortam sıcaklığı.
Çoğu metal için normal sıcaklıktaki özdirenç bununla orantılıdır, yani p ~ T. Ancak düşük sıcaklıklarda sapmalar gözlenir. 0°K'ye yakın sıcaklıklarda çok sayıda metal ve alaşım için direnç hesaplaması sıfır değerleri gösterdi. Bu fenomene süperiletkenlik denir. Örneğin, cıva, kalay, kurşun, alüminyum vb. bu özelliğe sahiptir. Her metalin süperiletkenlik olgusunun gözlemlendiği kendi kritik sıcaklığı Tk vardır.
Ayrıca, silindir özdirenci tanımının aynı malzemeden yapılmış tellere genelleştirilebileceğini unutmayın. Bu durumda, özdirenç formülündeki kesit alanı, telin kesitine ve l - uzunluğuna eşit olacaktır.






