Termodinamiğin önemli bir bölümü, bir maddenin farklı fazları arasındaki dönüşümlerin incelenmesidir, çünkü bu süreçler pratikte gerçekleşir ve belirli koşullar altında bir sistemin davranışını tahmin etmek için temel öneme sahiptir. Bu dönüşümlere, makalenin adandığı faz geçişleri denir.
Faz ve sistem bileşeni kavramı

Fizikte faz geçişlerini ele almadan önce, faz kavramını tanımlamak gerekir. Genel fizik dersinden bilindiği gibi maddenin üç hali vardır: gaz, katı ve sıvı. Bilimin özel bir bölümünde - termodinamikte - yasalar maddenin halleri için formüle edilir, kümelenme durumları için değil. Bir faz, homojen bir yapıya sahip, belirli fiziksel ve kimyasal özelliklerle karakterize edilen ve maddenin geri kalanından interfaz adı verilen sınırlarla ayrılan belirli bir madde hacmi olarak anlaşılır.
Böylece, "faz" kavramı, özellikler hakkında pratik olarak çok daha önemli bilgiler taşır.yığılma durumundan daha önemlidir. Örneğin, demir gibi bir metalin katı hali şu aşamalarda olabilir: düşük sıcaklıkta manyetik gövde merkezli kübik (BCC), düşük sıcaklıkta manyetik olmayan bcc, yüzey merkezli kübik (fcc) ve yüksek- sıcaklık manyetik olmayan bcc.
"Faz" kavramına ek olarak, termodinamik yasaları, belirli bir sistemi oluşturan kimyasal elementlerin sayısı anlamına gelen "bileşenler" terimini de kullanır. Bu, fazın tek bileşenli (1 kimyasal element) veya çok bileşenli (birkaç kimyasal element) olabileceği anlamına gelir.
Gibbs' teoremi ve sistemin fazları arasındaki denge

Faz geçişlerini anlamak için aralarındaki denge koşullarını bilmek gerekir. Bu koşullar, dış etkilerden izole edilen sistemin toplam Gibbs enerjisi değişmeyi bıraktığında denge durumuna ulaşıldığı varsayılarak, her biri için Gibbs denklemleri sistemi çözülerek matematiksel olarak elde edilebilir.
Belirtilen denklem sisteminin çözülmesinin bir sonucu olarak, birkaç faz arasında dengenin varlığı için koşullar elde edilir: izole bir sistem ancak tüm fazlardaki basınçlar, her bileşenin kimyasal potansiyelleri ve sıcaklıklar oluştuğunda gelişmeyi durduracaktır. birbirine eşittir.
Denge için Gibbs faz kuralı

Birkaç fazdan ve bileşenden oluşan bir sistem sadece dengede olmayabilir.belirli koşullar altında, örneğin belirli bir sıcaklık ve basınçta. Denge için Gibbs teoremindeki bazı değişkenler, bu dengede bulunan hem faz sayısı hem de bileşen sayısı korunurken değiştirilebilir. Sistemdeki dengeyi bozmadan değiştirilebilen değişkenlerin sayısına bu sistemin serbestlik sayısı denir.
f faz ve k bileşenden oluşan bir sistemin l özgürlük sayısı, Gibbs faz kuralından benzersiz bir şekilde belirlenir. Bu kural matematiksel olarak şu şekilde yazılır: l + f=k + 2. Bu kuralla nasıl çalışılır? Çok basit. Örneğin sistemin f=3 denge evresinden oluştuğu bilinmektedir. Böyle bir sistemin içerebileceği minimum bileşen sayısı nedir? Soruyu şu şekilde akıl yürüterek cevaplayabilirsiniz: Denge durumunda, en katı koşullar, yalnızca belirli göstergelerde gerçekleştirildiğinde ortaya çıkar, yani herhangi bir termodinamik parametrede bir değişiklik dengesizliğe yol açacaktır. Bu, özgürlük sayısının l=0 olduğu anlamına gelir. Bilinen l ve f değerlerini değiştirerek, k=1 elde ederiz, yani üç fazın dengede olduğu bir sistem bir bileşenden oluşabilir. En iyi örnek, belirli sıcaklık ve basınçlarda buz, sıvı su ve buharın dengede olduğu suyun üçlü noktasıdır.
Faz dönüşümlerinin sınıflandırılması
Dengedeki bir sistemdeki bazı termodinamik parametreleri değiştirmeye başlarsanız, bir fazın nasıl kaybolacağını ve diğerinin nasıl görüneceğini gözlemleyebilirsiniz. Bu işlemin basit bir örneği, ısıtıldığında buzun erimesidir.
Gibbs denkleminin yalnızca iki değişkene (basınç ve sıcaklık) bağlı olduğu ve faz geçişinin bu değişkenlerde bir değişiklik içerdiği düşünüldüğünde, fazlar arasındaki geçiş, Gibbs enerjisinin değişkenler. Avusturyalı fizikçi Paul Ehrenfest tarafından 1933'te faz dengesindeki bir değişiklikle meydana gelen bilinen tüm termodinamik süreçlerin bir sınıflandırmasını derlerken kullandığı bu yaklaşımdı.
Termodinamiğin temellerinden, Gibbs enerjisinin sıcaklığa göre birinci türevinin sistemin entropisindeki değişime eşit olduğu sonucu çıkar. Gibbs enerjisinin basınca göre türevi hacimdeki değişime eşittir. Sistemdeki fazlar değiştiğinde, entropi veya hacim bir kesintiye uğrarsa, yani aniden değişirse, o zaman birinci dereceden bir faz geçişinden bahsederler.
Ayrıca, Gibbs enerjisinin sıcaklığa ve basınca göre ikinci türevleri sırasıyla ısı kapasitesi ve hacimsel genleşme katsayısıdır. Fazlar arasındaki dönüşüme, belirtilen fiziksel niceliklerin değerlerinde bir süreksizlik eşlik ediyorsa, o zaman ikinci dereceden bir faz geçişinden söz edilir.
Aşamalar arasındaki dönüşüm örnekleri

Doğada çok sayıda farklı geçiş vardır. Bu sınıflandırma çerçevesinde, birinci tür geçişlerin çarpıcı örnekleri, sistemde bir hacim atlaması olduğunda metallerin eritilmesi veya su buharının havadan yoğuşması süreçleridir.
İkinci dereceden geçişlerden bahsedersek, çarpıcı örnekler, demirin bir sıcaklıkta manyetikten paramanyetik duruma dönüşümüdür.768 ºC veya mutlak sıfıra yakın sıcaklıklarda metalik bir iletkenin süper iletken duruma dönüşümü.
Birinci tür geçişleri açıklayan denklemler
Pratikte, bir sistemde faz dönüşümleri meydana geldiğinde sıcaklık, basınç ve emilen (serbest bırakılan) enerjinin nasıl değiştiğini bilmek genellikle gereklidir. Bunun için iki önemli denklem kullanılır. Termodinamiğin temel bilgilerine dayalı olarak elde edilirler:
- Farklı fazlar arasındaki dönüşümler sırasında basınç ve sıcaklık arasındaki ilişkiyi kuran Clapeyron formülü.
- Dönüşüm sırasında emilen (serbest kalan) enerji ile sistemin sıcaklığını birbirine bağlayan Clausius formülü.
Her iki denklemin kullanımı sadece fiziksel niceliklerin nicel bağımlılıklarının elde edilmesinde değil, aynı zamanda faz diyagramlarında denge eğrilerinin eğiminin işaretinin belirlenmesinde de kullanılır.
İkinci tür geçişleri açıklamak için denklem

1. ve 2. tür faz geçişleri farklı denklemlerle tanımlanır, çünkü Clausius ve Clausius denklemlerinin ikinci dereceden geçişler için uygulanması matematiksel belirsizliğe yol açar.
İkincisini tanımlamak için, dönüşüm işlemi sırasında ısı kapasitesindeki değişiklikler ve hacimsel genleşme katsayısı bilgisi aracılığıyla basınç ve sıcaklıktaki değişiklikler arasında bir ilişki kuran Ehrenfest denklemleri kullanılır. Ehrenfest denklemleri, manyetik alan yokken iletken-süper iletken geçişlerini tanımlamak için kullanılır.
Önemfaz diyagramları
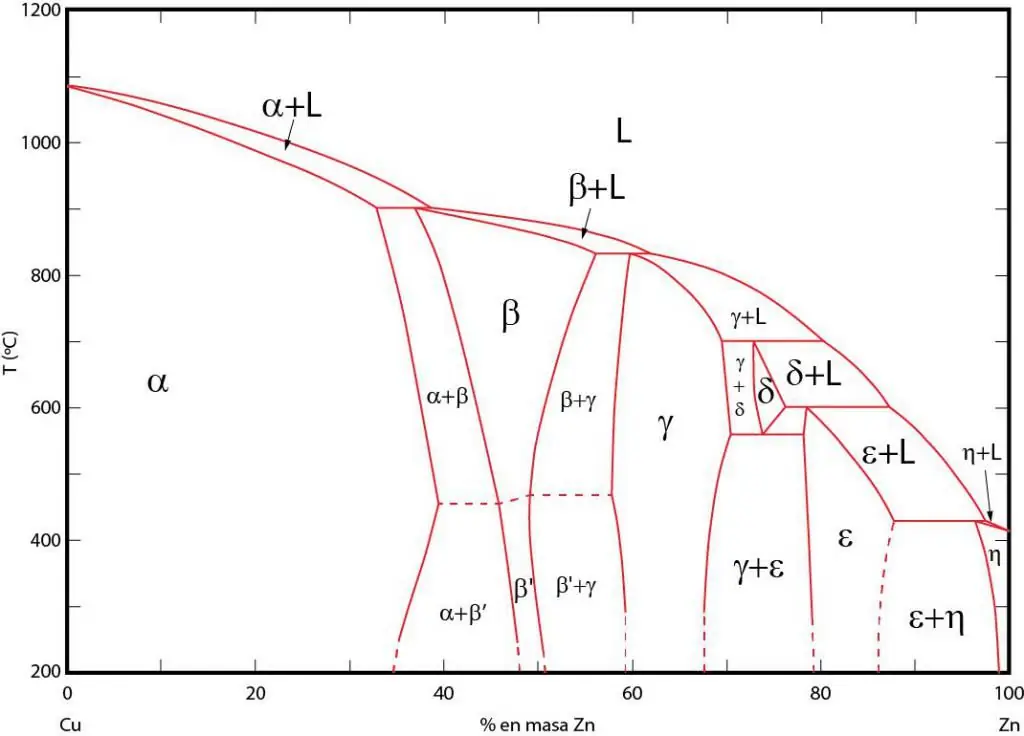
Faz diyagramları, karşılık gelen fazların dengede bulunduğu alanların grafik temsilidir. Bu alanlar fazlar arasındaki denge çizgileriyle ayrılır. P-T (basınç-sıcaklık), T-V (sıcaklık-hacim) ve P-V (basınç-hacim) faz diyagramları sıklıkla kullanılır.
Faz diyagramlarının önemi, dış koşullar buna göre değiştiğinde sistemin hangi aşamada olacağını tahmin etmenize izin vermesidir. Bu bilgiler, istenilen özelliklere sahip bir yapı elde etmek için çeşitli malzemelerin ısıl işlemlerinde kullanılmaktadır.






